DIFERENCIJALNI RACUN
Brzina
![]()
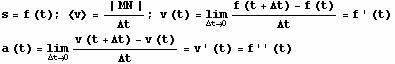
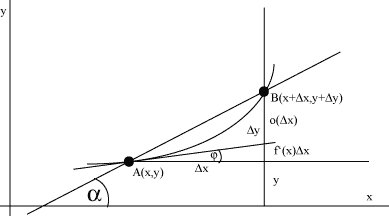
Tangenta krive
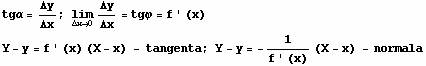
Definicija: Izvod
funkcije f:AŕR u tacki 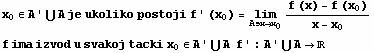
Definicija: f:AŕR je diferencijabilna u tacki
![]()
drugacje napisano:
![]()
Stav: Funkcija f je
diferencijabilna u tacki akko ima izvod u toj tacki.
Dokaz:![]()
![]()
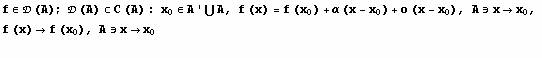
![]()
Primer: ![]()
Definicija (desni i
levi izvod):
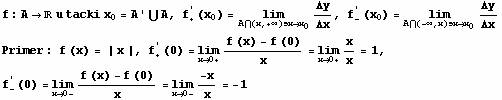
Tablica izvoda:
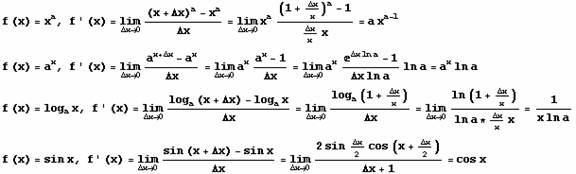
Stav (pravila
diferenciranja):

Stav (po izvodu
kompozicije):
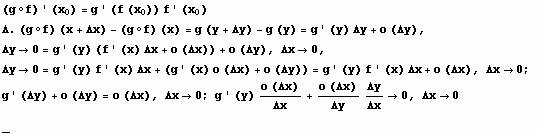
Stav (izvod inverzne
funkcije):
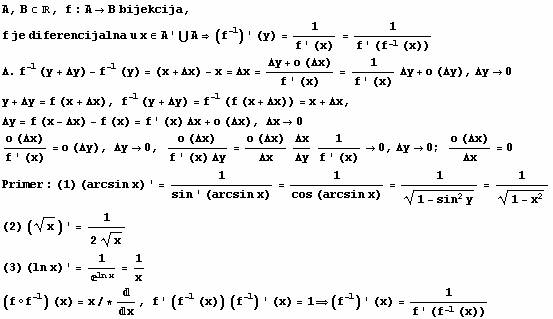
Osnovne teoreme diferencijalnog racuna
Fermaova Teorema:
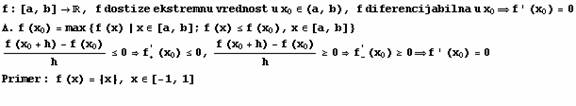 Rolova
Teorema:
Rolova
Teorema:

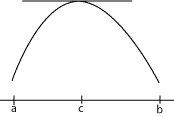
Kosijeva Teorema:

Lagranzova Teorema (o
srednjoj vrednosti):

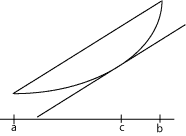
Primeri:
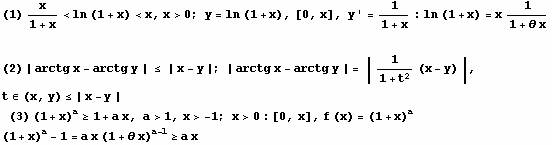
Posledica:
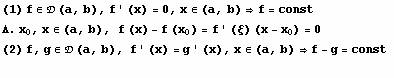
Stav:
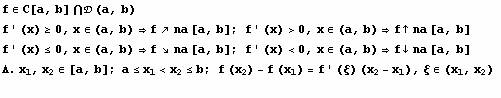
Stav:
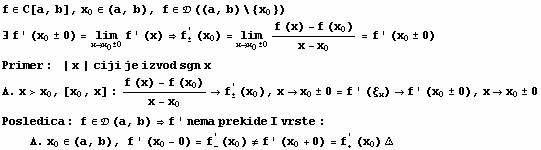
Darbuova Teorema:
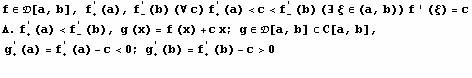
Funkcija je
neprekidna na zatvorenom, pa dostize ekstremum.

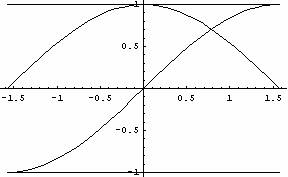
Lopitalovo pravilo:
![]()
Teorema:

Teorema:

Primeri:
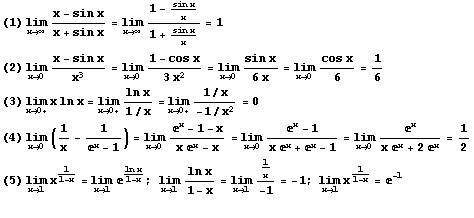
Visi izvodi
![]()
Lajbnicova formula
![]()
Tejlorova formula
Definicija:
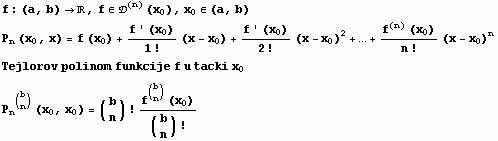
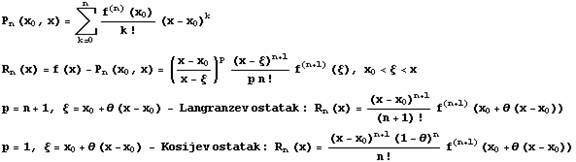
Teorema:
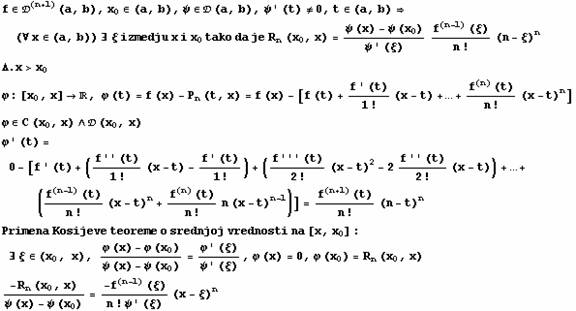
Posledice:
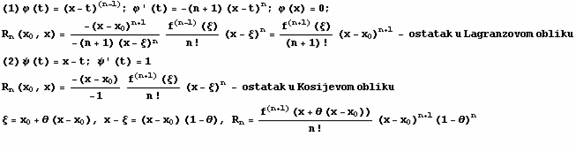
Stav (ostatak u
Peanovom obliku):

Meklorenovi razvoji ekstremnih funkcija
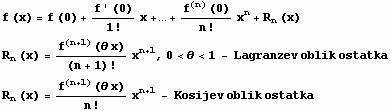
- Exp i trig –
Lagranz; Power, log – Kosi
- Za odredjivanje
ostataka stavlja se vrednost izmedju ostatka za θ=0
i θ=1.

Konveksne funkcije
![]()
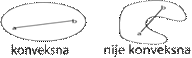
![]()
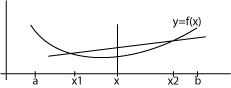
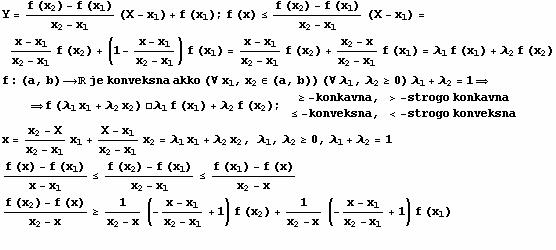
Stav:

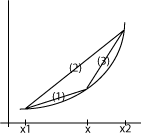
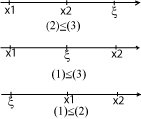
Stav:

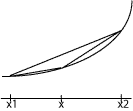
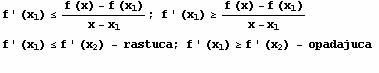
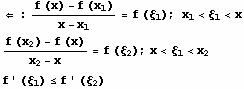
Stav:
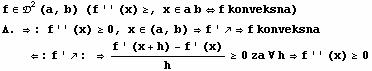
Stav:
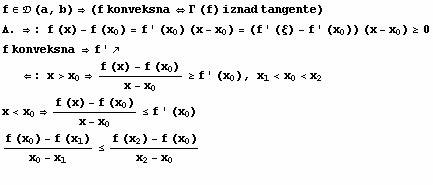
Ispitivanje funkcija
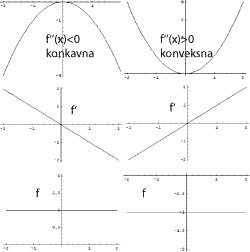
Definicija:
![]()
Stav:
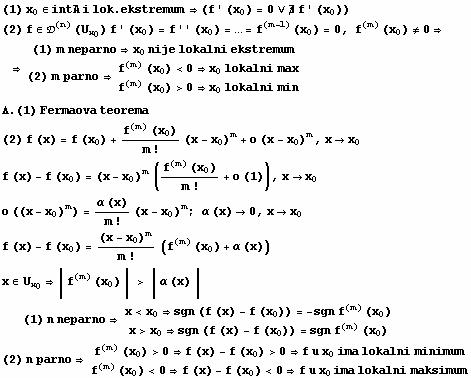
(1) Prema Fermaovoj
teoremi da bi diferencijabilna funkcija imala lokalni ekstremum u nekoj tacki
x0, neophodno je da njen izvod u toj tacki bude jednak nuli.
(2) Neka funkcija ima
u tacki x0 prvi izvod jednak nuli, i definisan drugi izvod. Ako je drugi izvod
u tacki x0 manji od nule, onda funkcija u tacki x0 ima lokalni maksimum, ako je
veci od nule, lokalni minimum.
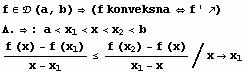
Definicija:
x0 je prevojna tacka
funkcije akko na nekoj okolini tacke x0 funkcija f menja konveksnost u toj
tacki.

Stav:

Asimptote

Graficko predstavljanje funkcije
1) domen, asimptote,
specificna svojstva (parnost, periodicnost, znak, nule…)
2) diferencijabilnost,
prvi izvod, tok u lokalnom ekstremumu
3) drugi izvod,
konveksnost i prevojne tacke