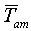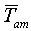 , koja se dobija računanjem srednje
vrednosti vremena pozicioniranja za sve moguće parove polaznog
i odredišnog cilindra. Konačni program, DISKCALC,
sa potpuno istom sintaksom argumentata kao program MODELS,
dat je uz ovaj domaći zadatak.
, koja se dobija računanjem srednje
vrednosti vremena pozicioniranja za sve moguće parove polaznog
i odredišnog cilindra. Konačni program, DISKCALC,
sa potpuno istom sintaksom argumentata kao program MODELS,
dat je uz ovaj domaći zadatak.
Za potrebe pronalaženja srednjeg vremena pristupa u slučaju da postoji više pristupnih mehanizama, napisao sam funkciju Simul koja simulira upravo ovakvu situaciju. Simulacijom se dobija srednje vreme pozicioniranja za milion simuliranih pristupa. Odredište svakog sledećeg pozicioniranja se dobija kao slučajan ceo broj u opsegu od nula do N-1 sa ravnomernom raspodelom, gde je N broj cilindara koje zauzima datoteka. U tome je i razlika između ovog programa i pregrama koji smo imali prilike da vidimo na predavanjima - tamo se simulira pristup kontinualnim modelom diska, a ovde diskretnim. Oba simulatora daju zadovoljavajuće približne rezultate. Tako, na primer za disk FUJITSU M228X se dobija:
Vrednosti za srednje Tam su:
Kontinualni model 1 daje: 25.848957
Kontinualni model 2 daje: 25.848957
Diskretni model daje: 25.863475
Rekurentna formula daje: 25.863475
Tacna vrednost je: 25.863475
Rezultati simulacije, n je broj pristupnih mehanizama:
n 1 2 3 4 5 6 7 8 9 10
Tam(n) [ms] 25.86 19.34 16.73 15.15 14.04 13.22 12.57 12.04 11.61 11.23
Zanimljivo je napomenuti da početni raspored mehanizama diska praktično ne utiče na dobijeni rezultat, ako je broj simuliranih pozicioniranja dovoljno veliki. Tako se za najnepovoljniji slučaj, kada su na početku simulacije svih mehanizmi pozicionirani na prvih nhds cilindara diska, dobija (za isti disk):
Rezultati simulacije, n je broj pristupnih mehanizama:
n 1 2 3 4 5 6 7 8 9 10
Tam(n) [ms] 25.87 19.35 16.73 15.14 14.04 13.21 12.57 12.04 11.60 11.23
Očigledno, nema značajne razlike u odnosu na prethodne rezultate. To se intuitivno može shvatiti ako se pretpostavi da nakon dovoljno velikog broja pozicioniranja srednji položaj mehanizama diska postaje konstantan, tako da početni razmeštaj unosi promenu samo kod nekoliko prvih pozicioniranja, a taj uticaj je utoliko manji ukoliko je ukupan broj simuliranih pristupa veći. Kako se u ovom programu simulira jedan milion pristupa, dolazimo do zaključka da se uticaj promene položaja praktično izgubi u srednjoj vrednosti.
Za moj disk, Western Digital AC540, dobija se:
Vrednosti za srednje Tam su: Kontinualni model 1 daje: 9.419267 Kontinualni model 2 daje: 9.419267 Diskretni model daje: 9.423852 Rekurentna formula daje: 9.423852 Tacna vrednost je: 9.423852 Rezultati simulacije, n je broj pristupnih mehanizama: n 1 2 3 4 5 6 7 8 9 10 Tam(n) [ms] 9.42 6.76 5.70 5.08 4.66 4.35 4.11 3.91 3.76 3.63
Funkciju za simuliranje sam dodao programu MODELS,
tako da se sada lako mogu porediti rezultati različitih modela
i simulacije. Takođe, dodao sam izračunavanje tačne vrednosti
za