(izvođenje parametara sistema)
uvod
Svakako najfascinantniji sistemi sa kojima se čovek sreće jesu oni čiji su elementi živa bića: biljke, životinje ili pak sami ljudi. Kompleksnost ovakvih sistema je oduvek fascinirala ljude a slož
enost zakonitosti koje vladaju u sistemu predstavljala vrhunski izazov za one koji su pokušavali da ih razumeju ili da sistemom upravljaju.Ovakve sisteme čovek je proučavao skoro tokom cele svoje istorije. Iako se nemože reći da su do kraja izučeni, ipak su neka pravila i zakonitosti ovakvih sistema odgonetnute. Dve su činjenice najvažnije u razumevanju funkcionisanja sistema:
Sem sistema živih bića postoje i drugi sistemi koji se povinuju sličnim zakonitostima i pravilima te se mogu posmatrati na analogan način. Svi oni se nazivaju sistemima sa rađanjem i umiranjem. To su sistemi iz oblasti saobraćaja, ekonomije ili pak računarskih nauka.
Ponašanje živih bića, pogotovo ljudi, se teško može opisati matematičkim jednačinama zbog mnoštva faktora koje treba uzeti u obzir kao i nepoznavanja posledica delovanja svih tih faktora. Zato ovi sistemi nisu podložni klasičnim matematičko-logičkim načinima analize. Sa druge strane, sistemi čiji su elementi vozila u saobraćajnom, novac u ekonomskom ili zahtevi u računarskom sistemu imaju (relativno) predvidljivije ponašanje i egzaktna pravila pa se mogu
analizirati matematički tj. statistički.U ovom tekstu biće posmatran računarski sistem i zahtevi /eng.
tasks, jobs, threads/ koje korisnici upućuju tom sistemu. Zahtevi dolaze u sistem (rađaju se), provode u njemu neko vreme i potom odlaze iz sistema (umiru). Stanje u kome se sistem nalazi, vreme koje će zahtevi provesti unutar sistema kao i ponašanje sistema kao celine najviše zavisi od broja zahteva i njihovog rasporeda. Dakle, vrlo slično već pomentim sistemima živih bića ali jednostavnije za analizu.Da bi se sprovela analiza ovakvog sistema, prvo se moraju uvesti izvesne početne postavke.
početne postavke i oznake
Prva pretpostavka koju treba uvesti je sasvim u skladu sa fizičkom ostvarljivošću sistema. Sistem mora biti ograničenog kapaciteta. Neka se,dakle, u njemu može u isto vrema nalaziti najviše
n zahteva gdeStanje
u kome se sistem nalazi označavaćemo sa Verovatnoću da se sistem nađe u stanju ![]() označićemo sa
označićemo sa ![]() . Za ove verovatnoće mora važiti:
. Za ove verovatnoće mora važiti:
![]()
Intenzitet prispeća zahteva u sistem označićemo sa
λ a intenzitet odlazaka zahteva iz sistema sa μ. Shodno drugoj pretpostavci, samtraćemo da su intenziteti prispeća i odlazaka zahteva zavisni od broja zahteva u sistemu j pa tako dakle imamo:![]() - intenzitet prispeća zahteva kada ima j zahteva u sistemu,
- intenzitet prispeća zahteva kada ima j zahteva u sistemu,
![]() - intenzitet odlazaka zahteva kada ima j zahteva u sistemu.
- intenzitet odlazaka zahteva kada ima j zahteva u sistemu.
Kako je ovaj sistem fizički, to važe sledeće restrikcije:
![]() (pun sistem),
(pun sistem),
![]() (prazan sistem).
(prazan sistem).
Treća pretpostavka je statističkog karaktera. Pretpostavićemo da se dva dolaska ili odlaska nemogu javiti (koincidirati) u isto vreme tj. preciznije u nekom kratkom vr
emenskom intervalu Δt. To znači da sistem iz stanjaNa osnovu ovih razmatranja možemo nacrtati graf prelaza ovakvog sistema.
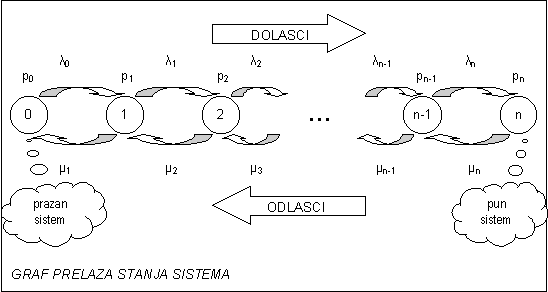
Eksponencijalni model rođenja i smrti
Iz uvodnog izlaganja i načinjenih pretpostavki sledi da se proces dolaska i odlaska zahteva iz sistema može modelovati Poasonovim slučajnim procesom. Za slučajnu veličinu X uzimamo broj procesa u sistemu.
Jednačina Poasonovog procesa glasi:
![]()
U ovom slučaju, u nekom jako kratkom vremenskom intervalu t, može se pojaviti najviše jedan novi zahtev:
![]()
Kada posmatrani vremenski interval t
teži nuli, izvod verovatnoće pojave i novih zahteva u sistemu je: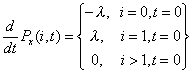
Kada je vreme t
jako malo, možemo koristiti oznaku dt. Sada verovatnoće pojave i zahteva u vremenskom intervalu dt možemo izračunati kao:![]() ,
,
![]() ,
,
![]() za i>1,
za i>1,
Isti rezon može se primeni
ti i na odlaske zahteva iz sistema. Tada bi umesto λ u gornjim jednačinama figurisalo μ.Verovatnoća da će sistem iz
j-tog preći u j+1 stanje jednaka je proizvodu verovatnoće da je sistem u stanju j i verovatnoće da se jedan novi proces pojavio. Shodno prethodnim jednačinama:![]()
Verovatnoća da će sistem iz stanja
j preći u stanje j-1 jednaka je proizvodu verovatnoće da je sistem u stanju j i verovatnoće da je jedan proces otišao iz sistema:![]()
Verovatnoću da se sistem nalazi u nekom
j-tom stanju možemo naći sledećim razmišljanjem: sistem je ili bio u j-tom stanju ili je u to stanje došao iz stanja j-1 odnosno j+1. Simbolično to možemo zapisati formulom:Pj[t+dt]=p(t){1-P[odlaska iz stanja j]}+P[dolaska u stanje j]
Izračunajmo sada verovatnoću da se sistem u trenutku
t+dt nađe u stanju j. Shodno prethodnim formulama sada dolazimo do konkretnih formula:![]()
![]() ;
;![]()
![]()
Izvodi gore nađenih verovotnoća glase:
![]()
![]()
![]()
Rezimirajmo sada početne uslove. Prvi uslov sledi iz definicije verovatnoće:
![]()
Drugi početni uslov kaže da se u trenutku t=0 sistem mora nalaziti u nekom početnom stanju jpoč koje se bira iz skupa stanja:
![]()
![]()
Treći početni uslov je
uslov statističkog ekvilibrijuma. Verovatnoće nalaženja sistema u stanju j nesmeju se menjati tokom vremena tj. biti funkcije vremena. U tom slučaju izvod verovatnoća pj po vremenu, u svakom trenutku, mora biti nula. Sistem se tada nalazi u statističkoj ravnoteži, što se matematički zapisuje kao:![]() , j=0,1,2, … ,n
, j=0,1,2, … ,n
Kao posledica trećeg početnog uslova sistem se sada uproštava:
![]()
![]()
![]()
Sada verovatnoće ![]() možemo izraziti preko
možemo izraziti preko ![]() i intenziteta prispeća/odlazaka zahteva
i intenziteta prispeća/odlazaka zahteva ![]()
![]()
![]()
![]() , j=1,2, … , n
, j=1,2, … , n
Primetimo da u gornjoj jednakosti važi:
![]()
što ustvari predstavlja uslov izbalansiranosti saobraćaja između stanja
j i j-1. Gledano u nekom dužem vremenskom intervalu, broj prelazaka sistema iz stanja j-1 u stanje j biće jednak broju prelazaka sistema iz stanja j u stanje j-1. Ova izbalansiranost je posledica trećeg početnog uslova tj. statističke ravnoteže sistema.Konačno, imajući u vidu gornji sistem dolazimo do formula rođenja
i smrti: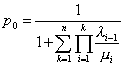
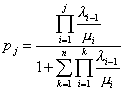
Parametri sistema
Značaj formula rođenja i smrti je u tome što one predstavljaju direktnu vezu između verovatnoća stanja u sistemu i intenziteta dolazaka tj. odlazaka zahteva iz sistema. Barem neka od tih veličina može se odrediti statistički (eksperimentom) a na osnovu formula onda i ostale. To bi bio praktičan značaj.
Teorijski zančaj ogleda se u mogućnosti da iz tih veličina iznađemo i neke
od parametara koji bi konkretnije okarakterisali posmatrani sistem. Ti parametri dati su dole.
prosečan broj zahteva u sistemu
Prosečan broj zahteva
J u posmatranom sistemu možemo odrediti kao matematičko očekivanje stanja u kome se sistem nalazi. Kako je stanje sistema prosta funkcija broja zahteva u njemu to imamo:![]()
produktivnost sistema
Produktivnost sistema /eng. throughput/ prestavlja intenzitet kojim zahtevi napuštaju sistem. Oz
načava se sa X a računa kao suma proizvoda intenziteta odlazaka zahteva i verovatnoće j-tog stanja sistema tj.![]()
iskorišćenost sistema
Iskorišćenost sistema, u oznaci
U, je jednostavno verovatnoća da sistem radi. Drugačije rečeno, sistem radi onda kad nije besposlen tj. kad ima bar jedan zahtev u njemu. Dakle:![]()
srednje vreme boravka zahteva u sistemu (Litlova formula)
Litlova /Little/ formula daje nam vezu
između prosečnog broja zahteva i njihovog srednjeg vremena boravka u posmatranom sistemu. Ove dve veličine su direktno srazmerne, gde je koeficijent srazmernosti ustvari produktivnost sistema:![]()
Dakle, posle nekog vremena T svih J
zahteva koji se nalaze u sistemu biće potpuno obrađeni.