POASONOV SLUČAJNI PROCES

(primena)

 

uvod

Teorija slučajnih procesa ili slučajnih funkcija vremena nalazi veliku primenu kako u elektrotehnici tako i u računarskim naukama. Jedna od primena ove teorije biće detaljnije iznesena u nastavku ovog teksta.

Kao uvod, biće navedeno nekoliko definicija:

Za neku slučajnu promenljivu X kaže se da ima Poasonovu raspodelu ako je ispunjeno:

,

gde kÎ {0,1,2, … } i λ>0.

Poasonova slučajna promenljiva služi kao model za broj telefonskih poziva u jedinici vremena, broj autobusa koji dolaze na neku stanicu u jedinici vremena, broj stabala neke šume po jedinici površine ili pak broj radioaktivnih raspada nekog materijala u jedinici vremena. Parametar λ predstavlja srednju vrednost ovih događaja, pa se tako i određuje.

Slučajan proces je familija slučajnih promenljivih {Xt}, tÎ T, pri čemu je T neki beskonačan skup. U primenama koje su ovde od interesa, indeks t prestavlja vreme. Za T se najčešće uzima interval [0, +∞) ili neki podskup ovog intervala. Ako je skup T diskretan, tada imamo niz slučajnih promenljivih ili proces sa diskretnim vremenom. U suprotnom imamo slučajni proces sa neprekidnim (kontinualnim) vremenom.

Poasonov proces je slučajni proces definisan na skupu T=[0, +∞) ako važi:

  1. P(X0=0)=1,

  2. priraštaji Xt-Xs i Xv-Xu su nezavisni za svako s<t≤u<v,

  3. za svako s,t (s<t), priraštaj Xt-Xs ima Poasonovu raspodelu sa parametrom λ(t-s) gde je λ pozitivna realna konstanta (λ>0).

 

 

osobine

Slučajni proces nazva se stacionarnim ako su njegove konačno dimenzionalne raspodele invarijantne u odnosu na translaciju u vremenu. Raspodele slučajnih vektora:

(Xt1, Xt2, … , Xtn) i (Xt1+s, Xt2+s, … , Xtn+s)

stacionarnog procesa su iste za svako s. Prostije rečeno, verovatnoća pojave događaja u segmentu [t,t+τ] je nezavisna od t i predstavlja funkciju samo od τ.

Odsustvo posledica ogleda se u sledećoj činjenici: vremenski intervali između neka dva događaja međusobno su nezavisni.

Ordinaran je onaj slučajni proces gde je verovatnoća da se u nekom jako kratkom vremenskom intervalu Δt (Δt→0) odigra više od jednog događaja zanemarljiva. Na drugi način rečeno, ta verovatnoća je mnogo manja od verovatnoće da se u tom intervalu odigra samo jedan događaj.

 

primena

Poasonovi procesi se primenjuju za modelovanje broja tzv. “retkih događaja”. Retki događaji su oni gde se u kratkom vremenskom intervalu može odigrati najviše jedan takav događaj. Ako sa Nt označimo broj događaja koji su se dogodili u vremenskom intervalu (0,t) onda je Nt Poasonov proces. U realne događaje koje ispunjavaju gornje uslove možemo ubrojati npr. broj telefonskih razgovora do trenutka t sa neke telefonske govornice, broj autobusa gradskog saobraćaja koji prođu pored nekog mesta ili pak broj zahteva koje korisnik uputi računarskom sistemu. U ovom smislu Poasonov proces se naziva i Poasonov protok događaja.

U daljem tekstu, biće detaljnije obrađen potok zahteva koje korisnici upućuju računarskom sistemu. Uvešćemo sledeće pretpostavke:

Cilj ovog izvođenja je da se pokaže da verovatnoća pojave i zahteva u nekom vremenskom intervalu t ima Posaonovu raspodelu.

 

izvođenje

Neka je sprovođenjem statističkog eksperimenta ustanovljeno da je u nekom vremenskom intervalu [0,T] prispelo N zahteva korisnika.

Srednji intenzitet prispeća zahteva je tada:

,

dok je srednje vreme između događaja:

ili

Verovatnoća da će korisnik podneti zahtev u nekom vremenskom intervalu t (t<T) je:

Od N prispelih zahteva moguće je formirati različitih rasporeda. Verovatnoća pojave i zahteva u vremenskom intervalu trajanja t ima, dakle, binomnu slučajnu raspodelu:

Kada T→+∞ imamo:

(1)

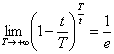
Verovatnoću pojave i zahteva sada možemo zapisati na sledeći način: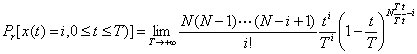

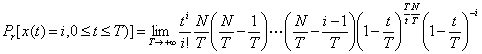
Koristeći činjenice da je , kao i jednakost (1) dolazimo do:

Pogodno je uvesti jednostavniju oznaku za veličinu Pr:

.

Verovatnoća Px(i,t) se takođe može izračunati uz pomoć rekurentne formule:

osobine

 

Za razliku od klasične definicije Poasonove raspodele u matematici gde je ona funkcija samo promenljive i, ovde imamo funkciju dve promenljive: broja zahteva i, te vremenskog intervala t. Broj zahteva je diskretna veličina, dok je vremenski interval kontinualna. To čini drugu razliku, jer je standardna Poasonova raspodela strogo diskretna.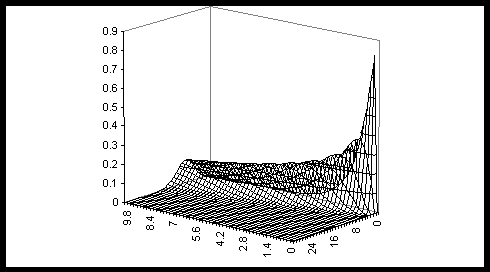

Na gornjoj slici prikazana je funkcija Px(i,t).

Ovu funkciju nije jednostavno analizirati klasičnim analitičkim metodama jer je jedan njen argument diskretan. Međutim, možemo se poslužiti nekim olakšicama.

Iz statistike je poznato da Poasonova raspodela dostiže svoj maksimum za:

,

za slučaj kada je λt ceo broj. Kada to nije slučaj, i se nalazi zaokruživanjem λt na najbliži ceo broj.

Analiza funkcije po promenljivoj t daje isti rezultat:

,

odakle se dobija:

.

Može se lako pokazati, da je funkcija Px(i,t) rastuća pa potom opadajuća po oba svoja argumenta zasebno. Ovo se takođe vidi i sa gornje slike, pa je gornji uslov stvarno uslov maksimuma.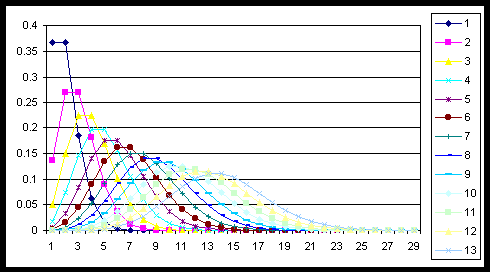

Na donjoj slici prikazane su funkcije Px(i,t), u zavisnosti od i za razne vrednosti λt.

 

 

parametri

Matematičko očekivanje Poasonove raspodele:

Varijansa (disperzija) Poasonove raspodele izračunava se pomoću alternativne definicije:

Matematičko očekivanje slučajne promenljive x2(t) nalazimo uz pomoć karakteristične funkcije Poasonove raspodele:

kao i teoreme:

.

Tako nalazimo da je:

odakle imamo:

 

 

é povratak na početak é