Od mnogobrojnih načina da opišemo kretanje glave hard diska, sa inžinjerske tačke gledišta, najprirodnije je krenuti od fizičkih osobina uređaja. Jedan od modela koji svoju polaznu tačku nalazi u fizici je kontinualni model baziran na fizičkim karakteristikama pristupnog mehanizma.

Spomenuti model razdvaja kretanje glave na 2 faze i opisuje ga kao linearno. Ovaj rad je pokušaj pravljenja modela koji kretanje pristupnog mehanizma deli na 4 faze, takođe uz linearne aproksimacije.

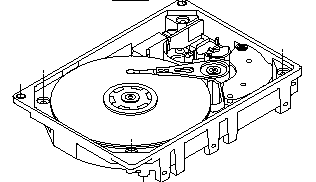
Poznavanje konstrukcije pristupnog mehanizma omogućava nam da, u nedostatku rezultata preciznih merenja, sačinimo nekoliko pretpostavki o kretanju magnetskih glava. Kao ilustraciju, možemo iskoristiti skicu unutrašnjosti jednog Seagate diska.

Prvo što možemo primetiti je da se magnetna glava nalazi na nosaču pričvršćenom za osovinu. Putanja glave se zato može opisati kao deo kružnice. Kako je poluprečnik diska manji od dužine nosača to putanja glave čini jako mali deo kružnice koji je vrlo blizak pravoj liniji.

Drugo, nosače i glave pokreće aktuator /actuator/, jedna vrsta motora koja omogućava brzo kontinualno pokretanje glave diska. To znači da je kretanje nosača prilčno nelinearno, tako da ga moramo detaljnije razmotriti.

Pretpostavićemo da magnetna glava u početnom trenutku miruje iznad neke, proizvoljne trake. Upravljački mehanizam diska dobija instrukciju da pročita sektor koji se nalazi na nekoj drugoj, takođe proizvoljnoj traci. Stoga on aktivira aktuator tako što mu šalje struju potrebnu za njegovo pokretanje.

Iz Osnova Elektrotehnike znamo da se struja kroz neko kolo nemože uspostaviti trenutno. Kako su motori električna kola koja sadrže velike induktivnosti, struja će se uspostavljati po eksponencijalnom zakonu. Sila i ubrzanje koje motor stvara direktno su srazmerni struji napajanja motora te se i oni menjaju po eksponencijalnom zakonu. Ovde moramo računati i sa trenjem. Iz Fizike znamo da je sila statičkog trenja mnogo veća od sile dinamičkog trenja što dodatno usporava pokretanje glave diska. Takođe, inerciju tela koje miruje teže je pobediti nego inerciju tela koje se kreće. Svi ovi faktori utiču da se ubrzanje pokretanje glave iz stanja mirovanja menja sporije nego što bi po eksponencijalnom zakonu promene struje trebalo.

U (kvazi)stacionarnom stanju struja napajanja motora postaje konstantna, definisana njegovom impedansom (tj. otpornošću). Sila i ubrzanje postaju konstantni a brzina linearno raste.

Ali sa povećanjem brzine raste i sila otpora sredine koja je ovoj direktno srazmerna, te još neki drugi neželjeni efekti koji smanjuju ubrzanje. U jednom trenutku, ako bi kretanje dovoljno dugo trajalo, dostigla bi se dovoljna brzina da se sila otpora sredine izjednači sa silom motora te bi ubrzanje postalo nula a brzina kontantna i to maksimalna koju aktuator može da postigne. Ali pitanje je da li kretanje glave može trajati toliko dugo da se se ta brzina postigne?

U svakom slučaju, u jednom trenutku, motor mora početi sa usporavanjem da bi se zaustavio na odgovarajućoj traci. Usporavanje motora može se postići ukidanjem sruje napajanja ili promenom njenog polariteta, što bi bilo efikasnije. Kako se struja kroz kolo nemože uspostaviti trenutno tako se nemože ni ukinuti tj. promeniti u trenutku. Energija akumulirana u induktivnostima motora učiniće da se promena struje vrši kontinualno takođe po eksponencijalnom zakonu. Ova promena traje neko izvesno, nezanemarljivo, vreme.

Na kraju, glava dolazi iznad ciljne trake. Pitanje koje se ovde postavlja je da li se glava može egzaktno zaustaviti baš iznad te trake? Mi ćemo pretpostaviti da najverovatnije nemože, tj. da pri dolasku na destinaciju, glava poseduje neku izvesnu brzinu i kinetičku energiju. Takođe, pretpostavićemo da je ta brzina veća što je veće rastojanje koje je glava prešla. Prostije rečeno, što je veći razmak između polazne i ciljne trake to glave razviju veću brzinu pa im je teže da “zakoče” pa se javlja izvestan “prebačaj”.

Aproksimirajući kretanje glava diska kao:

• pravolinijsko
• sa vremenski konstantnim ubrzanjem

možemo izvesti kontinualni model sa 2 faze. Te faze su:

Pročavajući prethodno opisani model, vidimo da on u ne uzima u obzir mnoge faktore koji se realno javljaju prilikom kretanja pristupnog mehanizma. Da bi neke od njih mogli da uzmemo u obzir, napravićemo kontinualni model sa 4 faze. Ovaj model bi predstavljao neku vrstu "nadogradnje" prethodnog modela.

Kretanje glave u 4 faze predstavićemo kao:

1. ubrzavanje ( a₁ = const )
2. konstantna (maksimalna) brzina ( v_max = const )
3. usporavanje (a₃ = const )
4. prigušeno oscilatorno kretanje

faza ubrzavanja

Ako zanemarimo početni period kada ubrzanje nije konstantno tj. smatrajući da je će ubrzanje dostići svoju maksimalnu vrednost za zanemarljivo kratko vreme – možemo ovu fazu smatrati potpuno ekvivalentnom prvoj fazi prethodnog modela.

Perod vremena u kome se ubrzanje glave menja od a₁ do a₃ nazvaćemo faza konstantne brzine i smatraćemo da se glava tada kreće maksimalnom brzinom v_max koju je dosegla na kraju prve faze.

Možemo sačiniti 2 pretpostavke o tome kakva je to konstantna brzina u ovoj fazi:

1. da je to izvesna maksimalna brzina od koje se glave diska nemogu kretati brže (zbog otpora sredine, trenja i dr.)
2. da je veoma mala promena brzine u ovoj fazi posledica nemogućnosti mehanizma da iz stadijuma ubrzavanja odmah pređe u stadijum usporavanja.

Dakle, ostaje nam da razmotrimo drugu pretpostavku. Neka sistem koji analiziramo čine aktuator i pristupni mehanizam. Ukupna energija sistema je suma kinetičke energije glava i energije sadržane u magnetnom polju kalema aktuatora (motora). Struja napajanja motora dodaje energiju magnetnom polju kalemova a oni je pretvaraju u kinetičku energiju glava. Kada promenimo struju napajanja motora, prilikom prelaska u fazu usporenja, ta promena se nemože izvršiti trenutno. Na račun energije sadržane u magnetnom polju indukovaće se neko vreme struja koja sprečava tu promenu. Energija sadržana u magnetnom polju nije velika i ona će se potrošiti za neko konačno (i uvek isto) vreme. Ali energija se takođe sadrži i u kretanju glava i pokušaj promene magnetnog polja povlači da počinje da se smanjuje kinetička energija glava na račun energije polja. U fazi usporavanja, proces prelaska kinetičke energije u magnetnu ograničen je faktorom snage aktuatora koju mi smatramo konstantnom. To znači da će se energija magnetnog polja ipak promeniti i da će se struja usporavanja I₃ ipak uspostaviti kroz izvesno vreme. To vreme je T₂ - vreme trajanja druge faze.

Deo kinetičke energije koji se u fazi 2 predaje magnetnom polju direktno je srazmeran izvodu po vremenu njene ukupne količine, E_kmax. Dakle, vreme prelaznog procesa direktno je srazmerno brzini u trenutku kada sistem ima maksimum kinetičke energije, tj. maksimalnoj brzini v_max. Matematički:

faza usporavanja

faza prigušenih oscilacija

Pretpostavićemo da glava hard diska nije u stanju da se egzaktno zaustavi iznad tačno određene trake, već da pri pokušaju pozicionioranja dolazi do “promašaja”. Takođe pretpostavićemo da se radi o “prebačaju” tj. da pri nailasku na ciljnu traku, glava nije stigla da se potpuno zaustavi i da nastavlja da se kreće. Kao posledica nastojanja mehanizma da glavu vrati na ciljnu traku, dolazi do prigušeno-oscilatornog kretanja glave.

Pitanje je koliko će glave “promašiti” cilnju traku? Imajući u vidu veliku nelinearnost karakteristike kretanja diska x(t), vidimo da je dosta teško tačno oceniti kada krenuti sa zaustavljanjem glave da bi ona stala na vreme tj. na određenom mestu. Intuitivno je jasno da što je veće rastojanje koje glava mora da pređe, to će biti teže postići dovoljnu preciznost u pozicioniranju pristupnog mehanizma.

.

Najveću kinetičku energiju, glave će imati u trenutku kada postignu maksimalnu brzinu. Sva energija stečena u fazi ubrzavanja, mora glavi biti oduzeta u fazi usporavanja. I ubrzanje i usporavanje glave zavise od brzine kojom motor dodaje/oduzima energiju dakle – od njegove snage. Snagu motora uzimamo kao konstantu.

Dakle, koliki će “promašaj” napraviti glave prilikom pozicioniranja, direktno zavisi od maksimalne kinetičke energije koju je glava postigla prilikom ubrzavanja, dakle – od kvadrata maksimalne brzine. Iz proračuna modela sa 2 faze namo da je maksimalna brzina proporcionalna korenu pređenog puta, pa je kvadrat v_max srazmeran samom pređenom putu x. Neka je dakle:

gde su: x₀ – rastojanje između ciljne i trake na kojoj se glava zaustavila,

Veličinu x₀ možemo usvojiti kao maksimalnu (početnu) amplitudu oscilatornog kretanja. Jednačina koja opisuje prigušeno oscilatorno kretanje, primenjena na ovaj slučaj glasi:

,

,

é povratak na početak é